Accueil > Acim-Maths : des outils > technique opératoire de la division
 technique opératoire de la division
technique opératoire de la division
samedi 18 mai 2019, par ,
par Henri Planchon et Marc-Olivier Roux
Cette modélisation montre « comment on fait une division » et garde la trace des étapes de l’algorithme.
La planche illustre le principe de la mise en schéma de techniques opératoires. Ce type de modélisation est destiné à favoriser la mentalisation et la mémorisation d’une procédure complexe, laquelle se trouve « mise à plat » et visualisée dans son ensemble, avec ses différentes étapes et ses calculs intermédiaires rendus « permanents ».
Ce qui est montré n’est pas une division prise comme exemple mais la structure qui est commune au calcul de toutes les divisions. L’enfant, l’adolescent, peuvent ainsi apprendre ou réapprendre à faire une division sans qu’il soit nécessaire de reprendre de longues explications orales.
Se trouve visualisée ici uniquement la « technique » de l’opération (procédure pour parvenir au résultat d’une division) et non pas le « sens de la technique » (justification de la procédure).
exploitation :
À gauche, quatre cases carrées : le dividende (à quatre chiffres). A droite, un triangle : le diviseur.
On colorie le contour du diviseur en rouge puis tous les autres triangles-diviseurs en rouge également (ces cases sont reliées entre elles). Colorier ensuite les autres éléments : les carrés en bleu, les ronds en vert, ...

On écrit une division, par exemple : 7634 divisé par 6 (un chiffre par case). Reporter le 6 dans les différents triangles.
Puis on suit la ligne du premier chiffre, 7 en l’occurence (règle : les cases reliées par un trait contiennent le même nombre). On arrive à :
7 = 6 x ... + ...
Il faut compléter cette écriture en inscrivant dans le rond et le carré les nombres qui conviennent (travail des répertoires multiplicatifs).
Ici : 7 = 6 x 1 + 1 (on vérifie que le complément est inférieur au diviseur).
Le complément (ici : 1) vient s’inscrire à côté du chiffre suivant issu du dividende (suivre les pointillés).
On a alors une nouvelle ligne :
16 = 6 x ... + ...
On complète : 16 = 6 x 2 + 4 puis on continue jusqu’en bas selon le même principe.
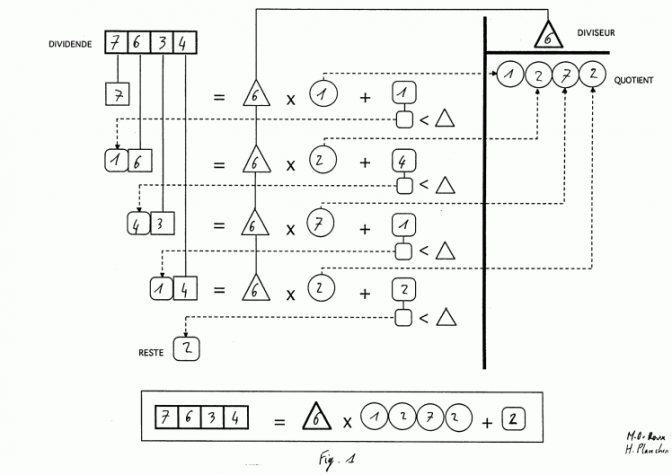
A la fin, les ronds constituent le résultat (quotient) de la division.
à noter :
En bas se trouve la règle qui permet de vérifier la division : dividende = quotient x diviseur + reste. Formule qui, en fait, a été appliquée pour les quatre lignes à compléter.
Pour les divisions avec deux chiffres au diviseur (par exemple 8587 divisé par 27), la procédure est la même : inscrire 27 dans le triangle et traiter successivement les lignes
8 = 27 x 0 + 8 ; puis 85 = 27 x 3 + 4, etc.
L’élève peut remplir les cases vides avec les nombres de son choix, sur autant d’exemples qu’il le veut, afin de vérifier que la procédure est bien générale et qu’elle « marche » dans tous les cas.
En pratique : on inscrit d’abord une division sur la planche, puis sur une feuille blanche en regardant la planche, puis sans la planche (une fois que le principe a été mémorisé). En cas d’oubli, reprendre la planche et retrouver la procédure.
La planche peut être téléchargée ici :
 ACIM
ACIM
